Introduction

In combination, modern computer hardware, algorithms and numerical methods are extraordinarily impressive. Take a moment to consider some simple examples, all using R.

1.
Simulate a million random numbers and then sort them into ascending order.
```
x <- runif(1000000)
system.time(xs <- sort(x))
```
```
##    user  system elapsed 
##   0.103   0.008   0.111
```
The sorting operation took 0.1 seconds on the laptop used to prepare these notes. If each of the numbers in x had been written on its own playing card, the resulting stack of cards would have been 40 metres high. Imagine trying to sort x without computers and clever algorithms.
2.
Here is a matrix calculation of comparatively modest dimension, by modern statistical standards.
```
set.seed(2)
n <- 1000
A <- matrix(runif(n*n),n,n)
system.time(Ai <- solve(A))  # invert A
```
```
##    user  system elapsed 
##   0.226   0.044   0.078
```
```
range(Ai%*%A-diag(n))        # check accuracy of result
```
```
## [1] -1.222134e-12  1.292300e-12
```
The matrix inversion took under half a second to perform, and the inverse satisfied its defining equations to around one part in . It involved around 2 billion () basic arithmetic calculations (additions, subtractions multiplications or divisions). At a very optimistic 10 seconds per calculation this would take 86 average working lives to perform without a computer (and that’s assuming we use the same algorithm as the computer, rather than Cramer’s rule, and made no mistakes). Checking the result by multiplying the A by the resulting inverse would take another 86 working lives.
3.
The preceding two examples are problems in which smaller versions of the same problem can be solved more or less exactly without computers and special algorithms or numerical methods. In these cases, computers allow much more useful sizes of problem to be solved very quickly. Not all problems are like this, and some problems can really only be solved by computer. For example, here is a scaled version of a simple delay differential equation model of adult population size, $n$ , in a laboratory blowfly culture.
$\frac{{\rm d} n}{{\rm d} t} = PT_ D n(t-1) e^{-n(t-1)} - \delta T_ D n(t).$
The dynamic behaviour of the solutions to this model is governed by parameter groups $PT_ D$ and $\delta T_ D$ , but the equation can not be solved analytically, from any interesting set of initial conditions. To see what solutions actually look like we must use numerical methods.
```
install.packages("PBSddesolve") ## install package from CRAN
```
```
library(PBSddesolve)

bfly <- function(t,y,parms) {
## function defining rate of change of blowfly population, y, at
## time t, given y, t, lagged values of y form ‘pastvalue’ and
## the parameters in ‘parms’. See ‘ddesolve’ docs for more details.

## making names more useful ...
  P <- parms$P;d <- parms$delta;y0 <- parms$yinit

  if (t<=1) y1 <- P*y0*exp(-y0)-d*y else { ## initial phase
    ylag <- pastvalue(t-1)         ## getting lagged y
    y1 <- P*ylag*exp(-ylag) - d*y  ## the gradient
  }
  y1  ## return gradient
}

## set parameters...
parms <- list(P=150,delta=6,yinit=2.001)
## solve model...
yout <- dde(y=parms$yinit,times=seq(0,15,0.05),func=bfly,parms=parms)
## plot result...
plot(yout$t,yout$y,type="l",ylab="n",xlab="time")
```
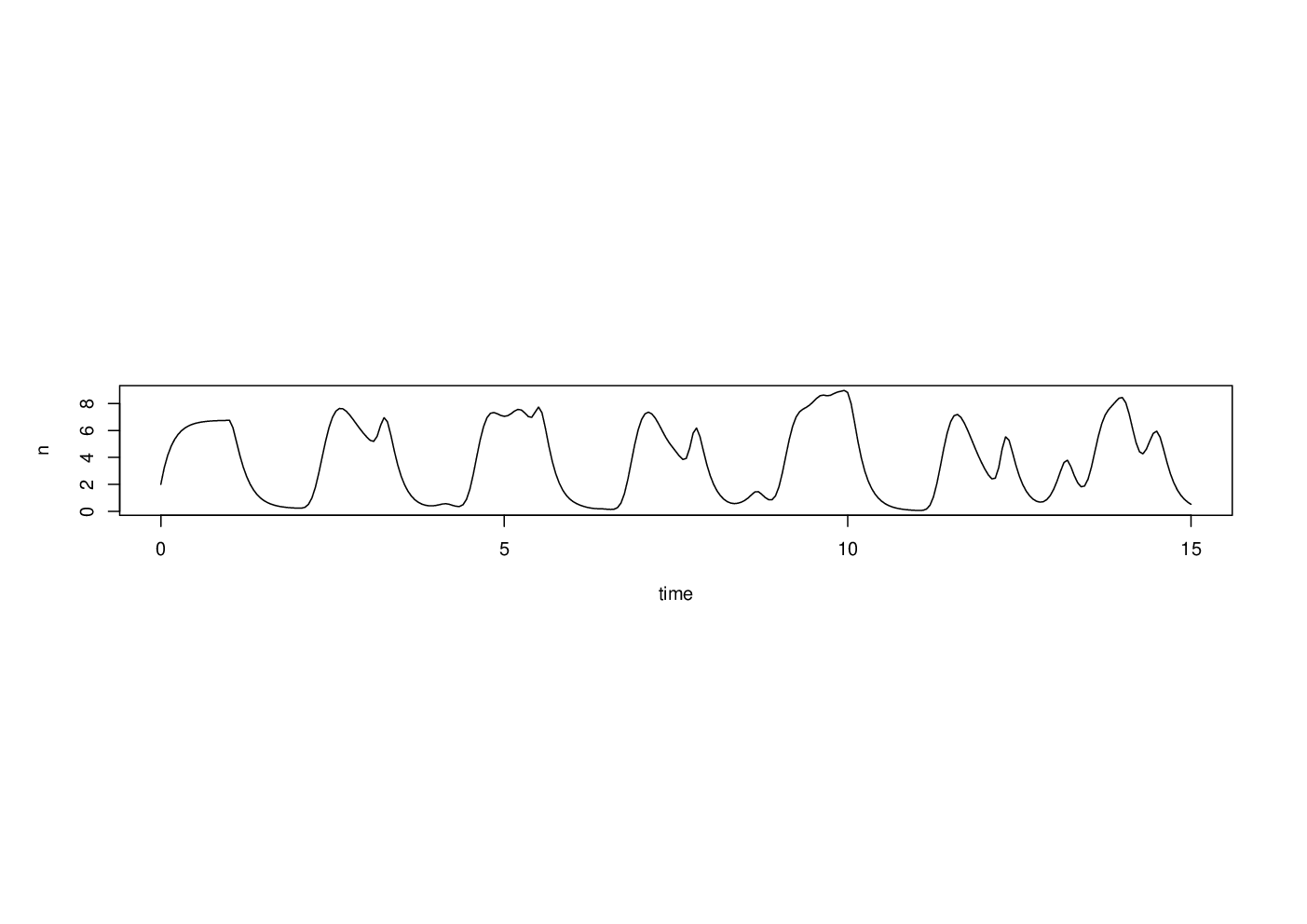
Here the solution of the model (to an accuracy of 1 part in $10^8$ ), took a quarter of a second.

1.1 Things can go wrong

The amazing combination of speed and accuracy apparent in many computer algorithms and numerical methods can lead to a false sense of security and the wrong impression that in translating mathematical and statistical ideas into computer code we can simply treat the numerical methods and algorithms we use as infallible ‘black boxes’. This is not the case, as the following three simple examples should illustrate.

The function in R measures how long a particular operation takes to execute. First generate two $3000 \times 3000$ matrices, ${\bf A}$ and ${\bf B}$ and a vector, ${\bf y}$ .

n <- 3000
A <- matrix(runif(n*n),n,n)
B <- matrix(runif(n*n),n,n)
y <- runif(n)

Now form the product $\bf ABy$ in two slightly different ways

system.time(f0 <- A%*%B%*%y)

##    user  system elapsed 
##   2.691   0.094   0.709

system.time(f1 <- A%*%(B%*%y))

##    user  system elapsed 
##   0.081   0.044   0.032

f0 and f1 are identical, to machine precision, so why is one calculation so much quicker than the other? Clearly anyone wanting to compute with matrices had better know the answer to this.

Note that system.time is a very crude method for benchmarking code. There are various R packages that can facilitate benchmarking and profiling of R code. Here we illustrate use of the rbenchmark package, which is available on CRAN.

library(rbenchmark)
benchmark(
    "ABy" = {
        f0 <- A%*%B%*%y
    },
    "A(By)" = {
        f1 <- A%*%(B%*%y)
    },
    replications = 10,
    columns = c("test", "replications", "elapsed",
                "relative", "user.self", "sys.self"))

##    test replications elapsed relative user.self sys.self
## 2 A(By)           10   0.295      1.0     0.864    0.311
## 1   ABy           10   7.552     25.6    27.638    1.868

2.
It is not unusual to require derivatives of complicated functions, for example when estimating models. Such derivatives can be very tedious or difficult to calculate directly, but can be approximated quite easily by ‘finite differencing’. i.e. if $f$ is a sufficiently smooth function of $x$ then
$\frac{\partial f}{\partial x} \simeq \frac{f(x+\Delta ) - f(x)}{\Delta }$
where $\Delta$ is a small interval. Taylor’s theorem implies that the right hand side tends to the left hand side, above, as $\Delta \to 0$ . It is easy to try this out on an example where the answer is known, so consider differentiating $\sin (x)$ w.r.t. x.
```
x <- seq(1,2*pi,length=1000)
delta <- 1e-5      # FD interval
dsin.dx <- (sin(x+delta)-sin(x))/delta # FD derivative
error <- dsin.dx-cos(x)     # error in FD derivative
```
The following plots the results. On the LHS is dashed, it’s true derivative is dotted and the FD derivative is continuous. The RHS shows the difference between the FD approximation and the truth.

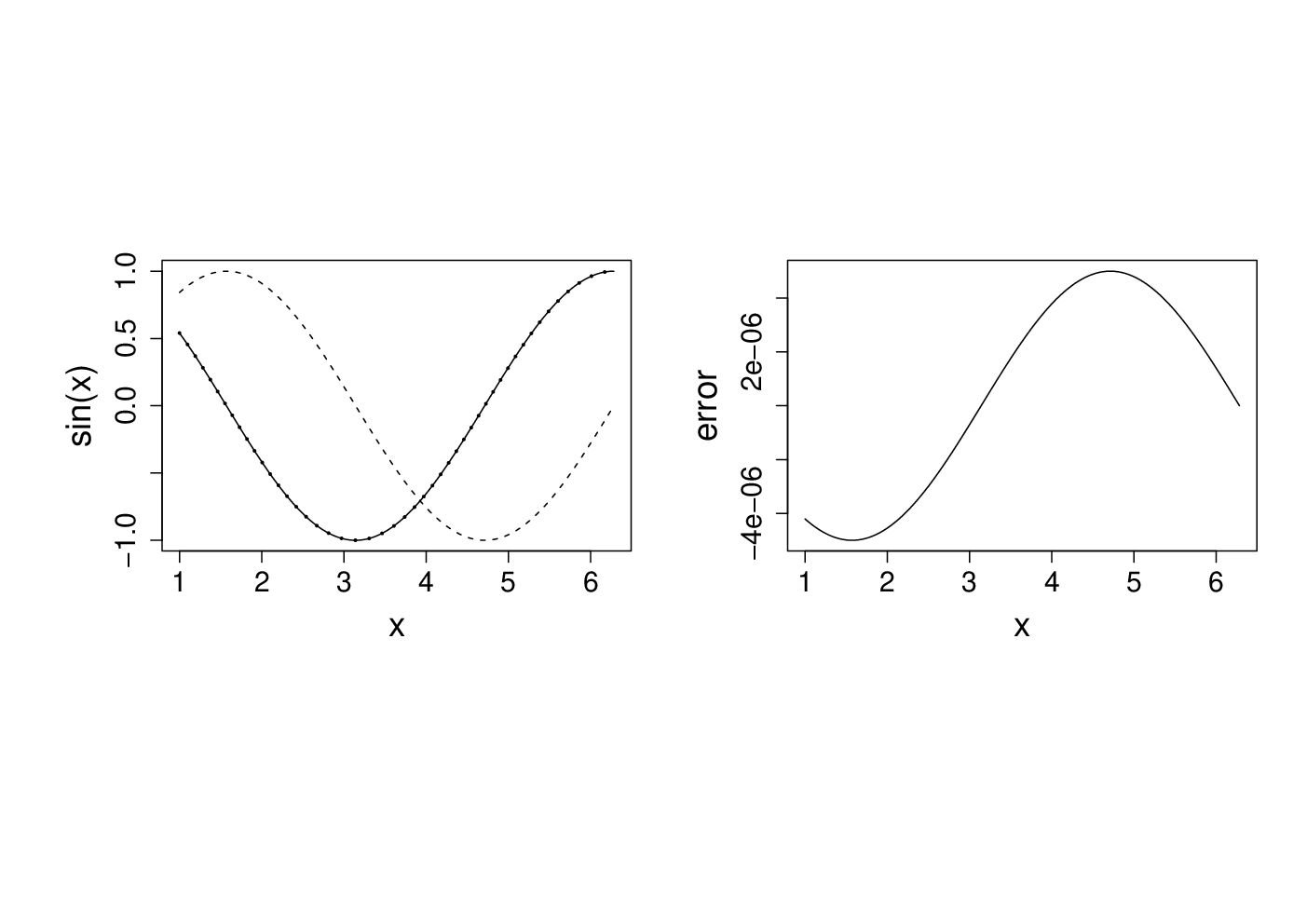
Note that the error appears to be of about the same magnitude as the finite difference interval $\Delta$ . Perhaps we could reduce the error to around the machine precision by using a much smaller $\Delta$ . Here is the equivalent of the previous plot, when
```
delta <- 1e-15
```
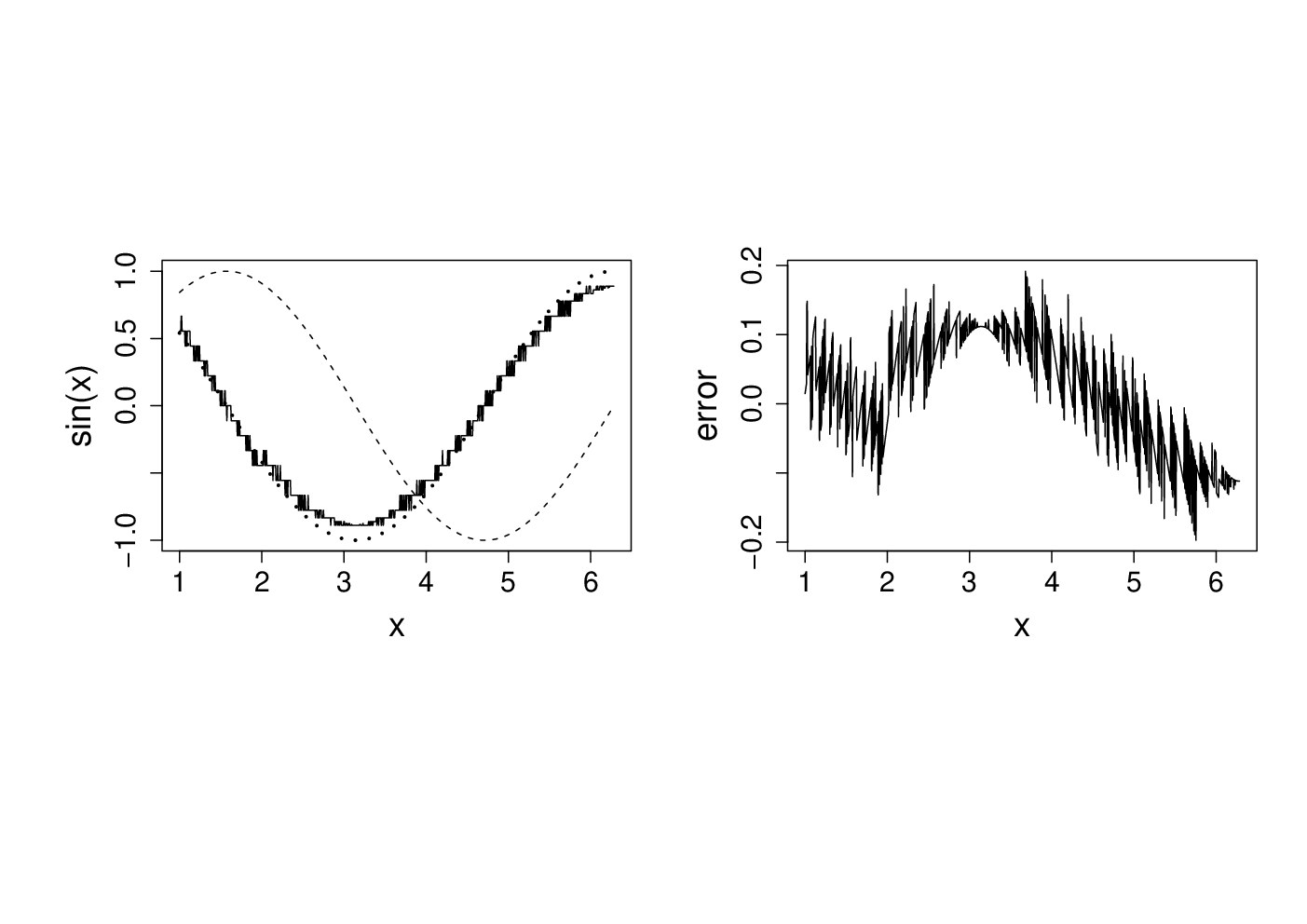
Clearly there is something wrong with the idea that decreasing $\Delta$ must always increase accuracy here.
3.
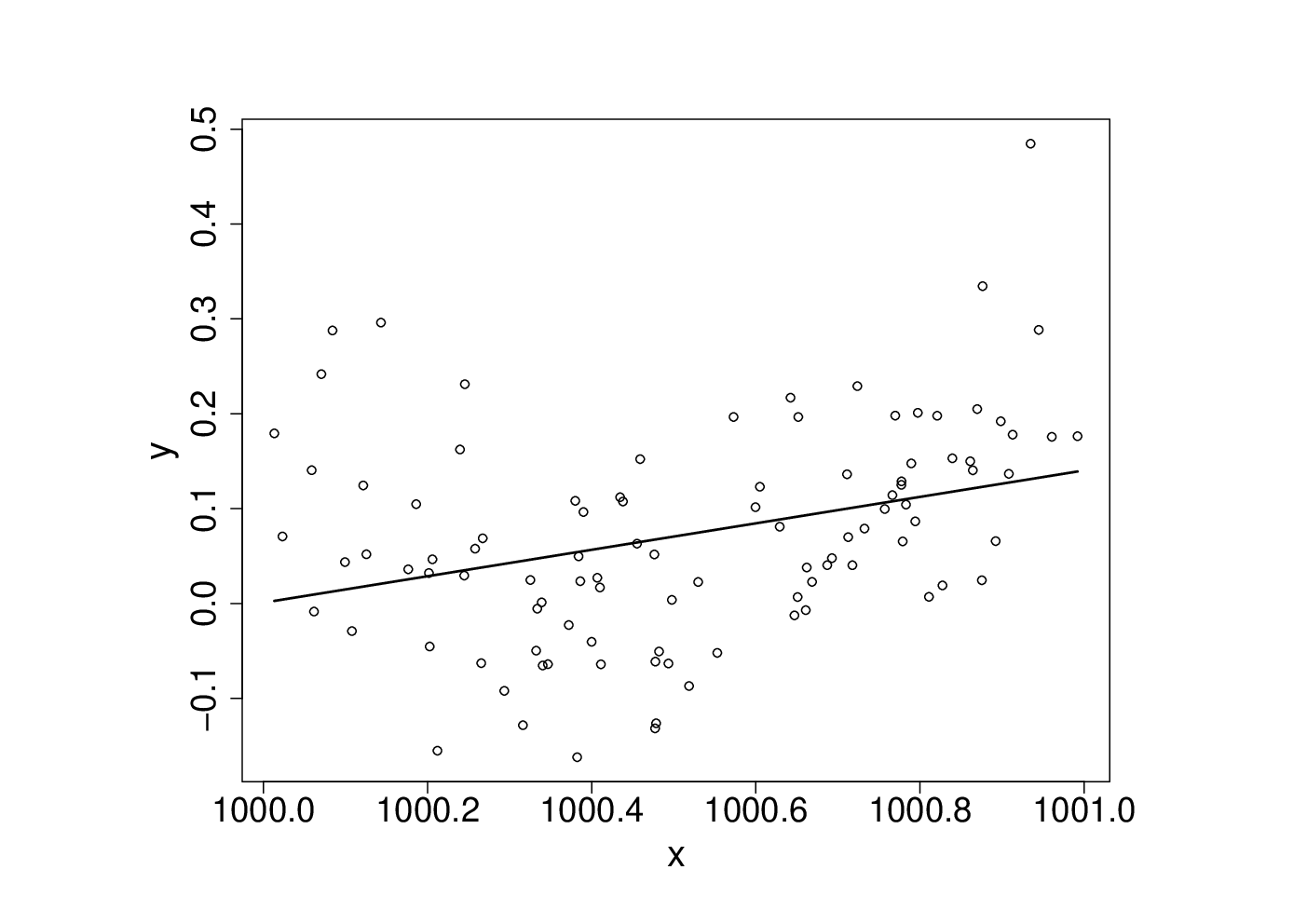
These data

were generated with this code…
```
set.seed(1); n <- 100
xx <- sort(runif(n))
y <- .2*(xx-.5)+(xx-.5)^2 + rnorm(n)*.1
x <- xx+100
```
An appropriate and innocuous linear model for the data is , where the are independent, zero mean constant variance r.v.s and the are parameters. This can be fitted in R with
```
b <- lm(y~x+I(x^2))
```
which results in the following fitted curve.

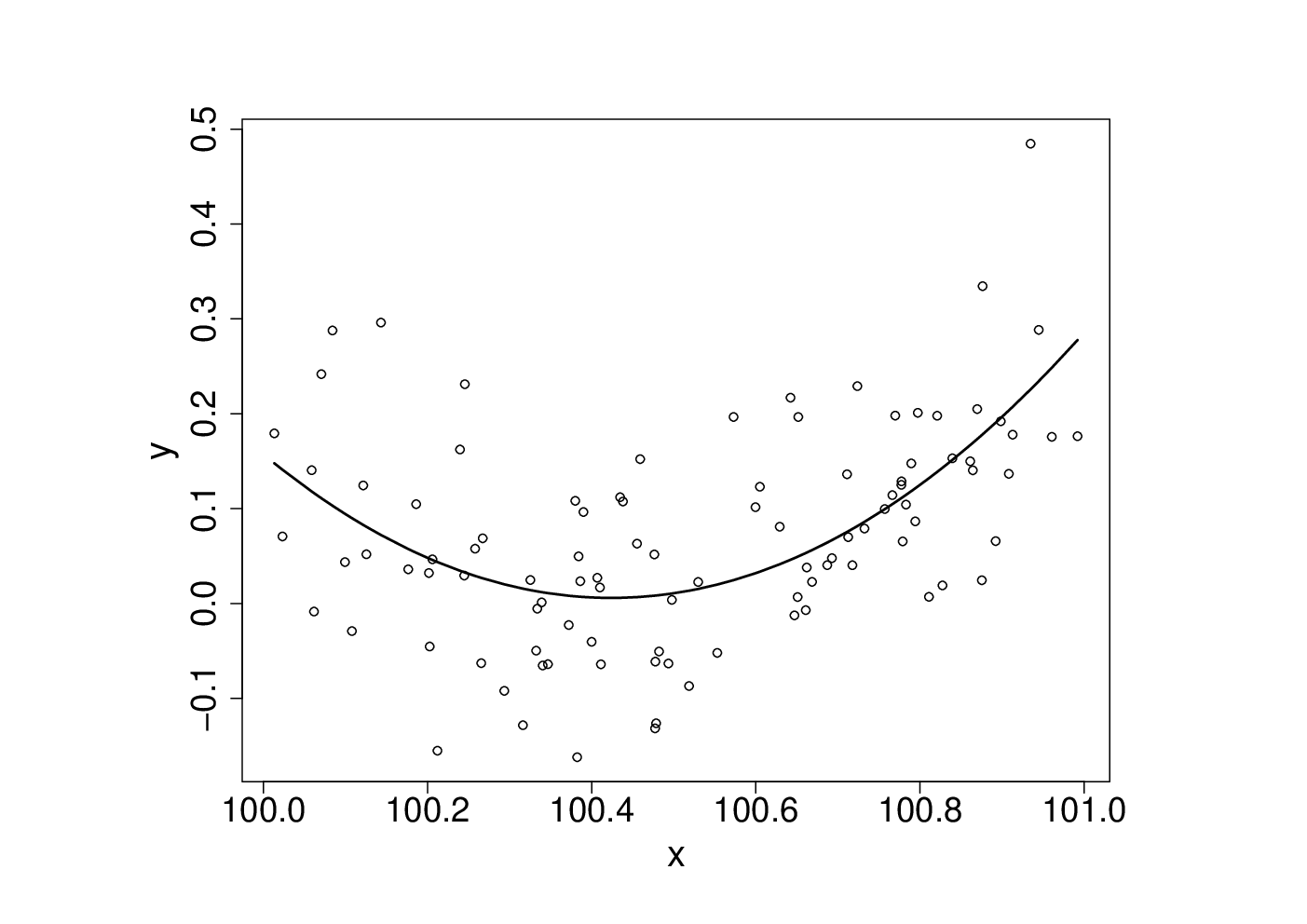
From basic statistical modelling courses, recall that the least squares parameter estimates for a linear model are given by $\hat{\bm \beta }= ({\bf X}^{\sf T}{\bf X})^{-1}{\bf X}^{\sf T}{\bf y}$ where ${\bf X}$ is the model matrix. An alternative to use of would be to use this expression for $\hat{\bm \beta }$ directly.
```
X <- model.matrix(b)    # get same model matrix used above
beta.hat <- solve(t(X)%*%X,t(X)%*%y) # direct solution of ‘normal equations’
```
## Error in solve.default(t(X) %*% X, t(X) %*% y): system is computationally singular: reciprocal condition number = 3.98647e-19
Something has gone badly wrong here, and this is a rather straightforward model. It’s important to understand what has happened before trying to write code to apply more sophisticated approaches to more complicated models.

In case you are wondering, I can make lm fail to. Mathematically it is easy to show that the model fitted values should be unchanged if I simply add 900 to the x values, but if I refit the model to such shifted data using lm, then the following fitted values result, which can not be correct.