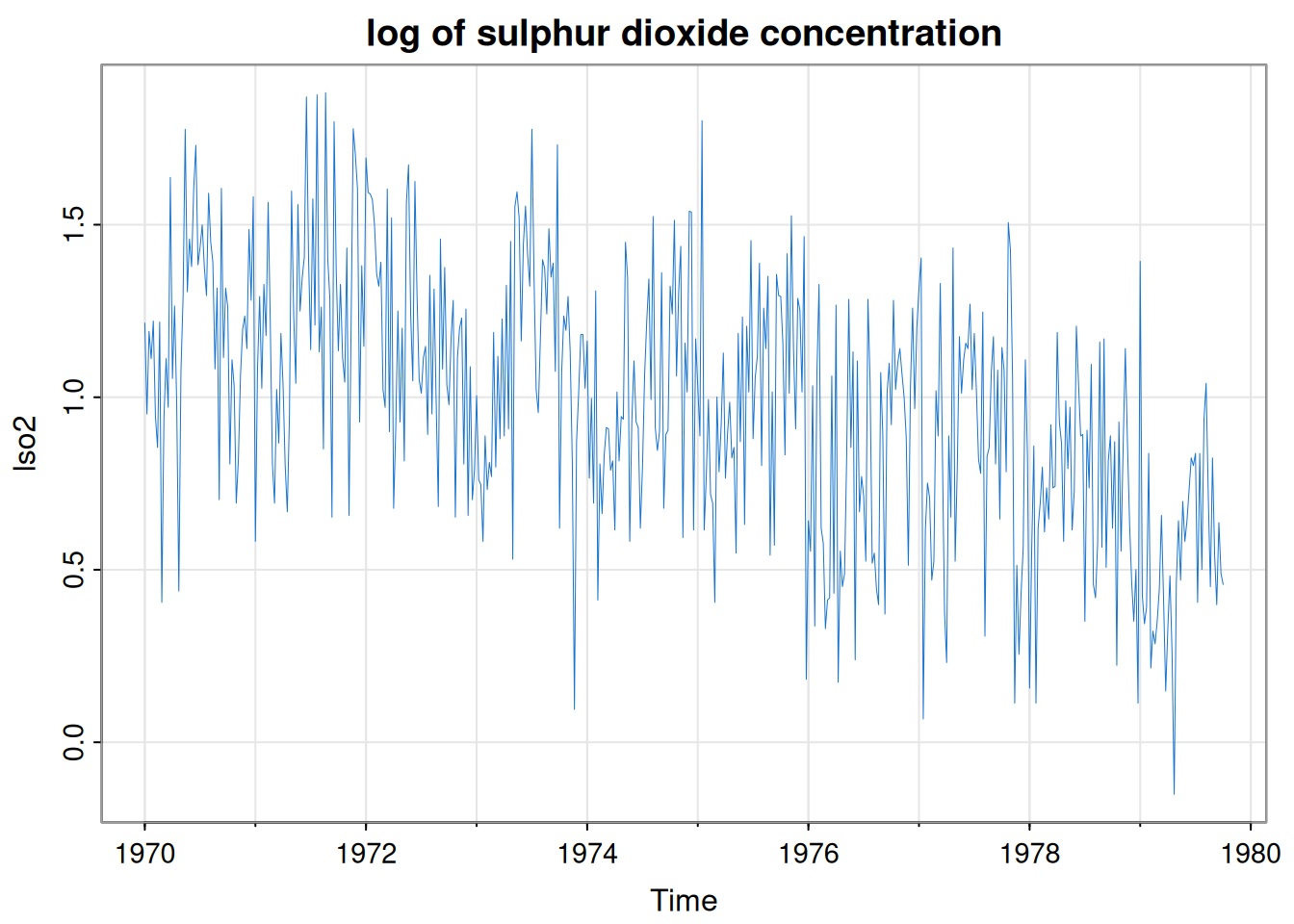
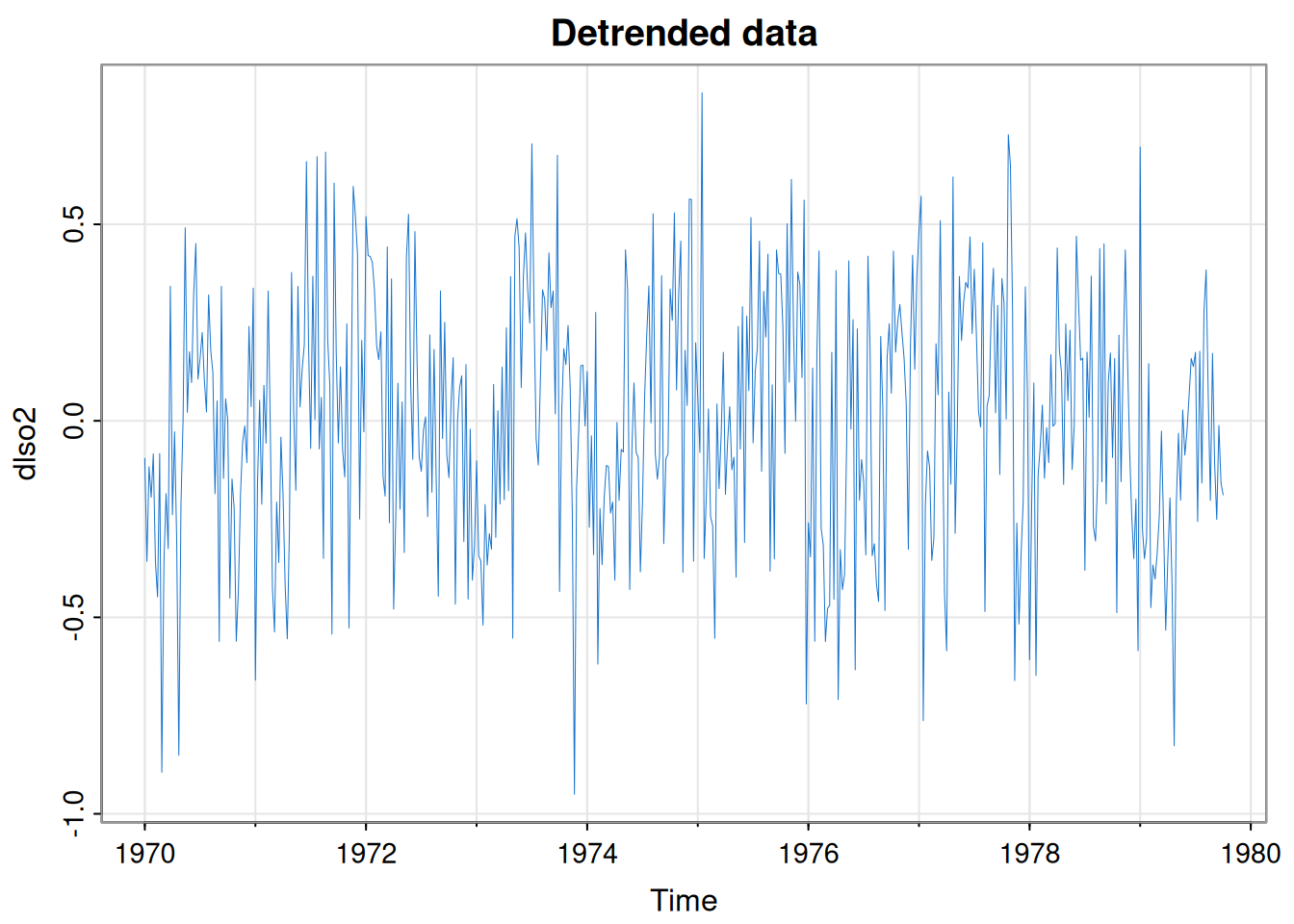
Overview
This lab document is an R Markdown file. It should be downloaded to your computer, and then loaded up into RStudio. Follow the instructions provided, writing code to solve the required problems into the provided code blocks, as directed. Regularly check on progress by “knitting” the document to a PDF and checking that the output is correct. You may find it helpful to have a separate R session window for writing, testing and debugging code solutions, before pasting back into the markdown document - that is up to you. But do make sure that all of your solutions are in this markdown document in the indicated places in the code blocks and that the document compiles into a PDF correctly.
This practical is constructed in a similar way to the practical test that will take place in week 10 (although this practical is shorter, to attempt to fit into a 50 minute session). At the end of the real test in week 10, you will compile your completed document to a PDF file and upload the PDF file (only) to Gradescope for marking. For this practical, you should make sure that you are able to compile your document to a PDF, but you don’t need to upload anything anywhere at the end of the session. You should simply check later that your completed PDF looks similar to the solution file that will be provided after the session.
Note that whilst the week 10 test will be conducted under exam conditions (ie. silence, no cooperation), during this lab it’s fine to discuss with your neighbours or ask for my help if you get stuck. Although the real test will be conducted in exam conditions, it will be open-book. You will be able to consult your lecture notes and other material on Blackboard Ultra that relates directly to this module. You should not use AI assistants.